Problem of the Week

Problem 8 hint

Nobody has yet submitted a satisfactory solution to Problem 8.

(i) You need to use the inequality on $\theta$ to show that $\sin\theta$ is not the negative square root of $1-(\cos\theta)^2$ . ( $\sqrt{x}$ means the non-negative square root of $x$ .)
(ii) You may only use the cosine rule and the given facts about $a$ , $b$ , $c$ , $\alpha$ , $\beta$ and $\gamma$ . You may not use any geometric properties of triangles beyond the cosine rule.
This means you must prove that $\cos(\alpha+\beta)=-\cos\gamma$ and $\alpha,\beta\le90^\circ$ for any numbers $\alpha$ , $\beta$ and $\gamma$ such that

$a^2 = b^2 + c^2 - 2bc\cos\alpha$ ,
$b^2 = a^2 + c^2 - 2ac\cos\beta$ ,
$c^2 = a^2 + b^2 - 2ab\cos\gamma$ ,
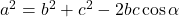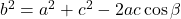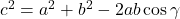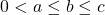$0 < a \le b \le c$ and
$0 \le \alpha \le \beta \le \gamma \le 180^\circ$ .

(Part (i) and the identity $\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$ , which holds for any values of $\alpha$ and $\beta$ , may help you prove this.)
(iii) Deduce from (ii) that $\cos(\alpha+\beta)=\cos(180^\circ-\gamma)$ and then use inequalities in $\alpha$ , $\beta$ and $\gamma$ along with the shape of the graph of $y=\cos x$ to show that $\alpha+\beta=180^\circ-\gamma$ .