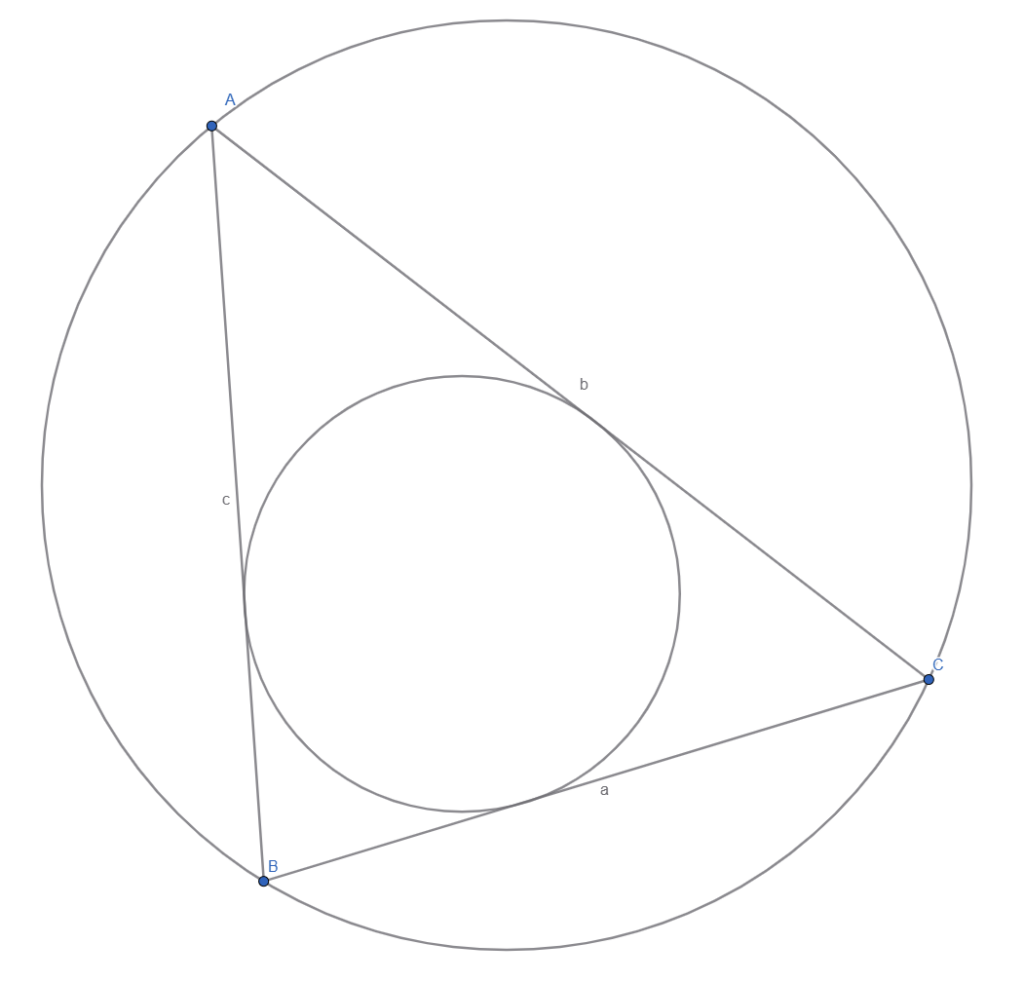
A triangle is inscribed in a circle, with it’s vertices on the circumference labelled A, B and C and their opposite sides labelled a, b and c respectively.
Within the triangle, the incircle is drawn, which is the largest circle that can fit inside the triangle. It is tangent to all three sides of the triangle.
The radius of the larger circle is labelled R while the radius of the smaller circle is labelled r.
A student would like to find the ratios between the radii of the two circles.
ai) Express 
in terms of 
and 
.
aii) Show that the area of the triangle can be represented by 
.
b) Express 
in terms of and the sine of all three angles.
ci) Hence find the ratio 
in terms of the sines of three angles.
cii) Evaluate the ratio when the inscribed triangle is an equilateral triangle.