Facebook Twitter Instagram

Problem of the Week

Problem 25 Solution

Congratulations to Markus Kuan from Northstowe Secondary College, Evie Somerville from King James Academy Royston and Henry Boulton for successfully solving the problem!

Let the centre circle be circle C. Let 2 of the adjacent circles be circles A and B.

a)

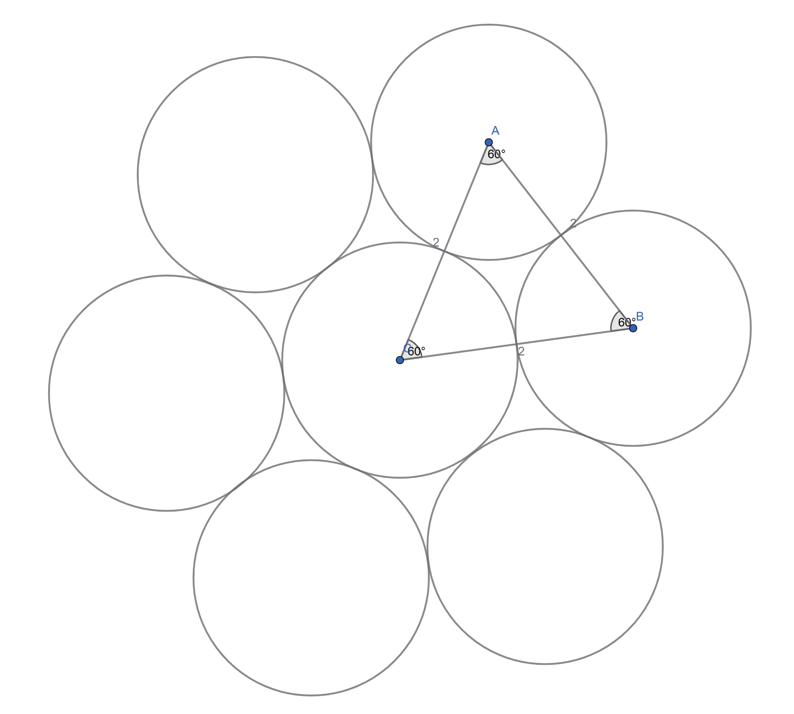
Each circle has radius 1, so AB = BC = AC = 2.

Triangle ABC is therefore equilateral.

Angle ACB = 60^\circ

Angles at a point = 360^\circ, therefore 360/60 = 6 circles can fit around the centre circle.

b)

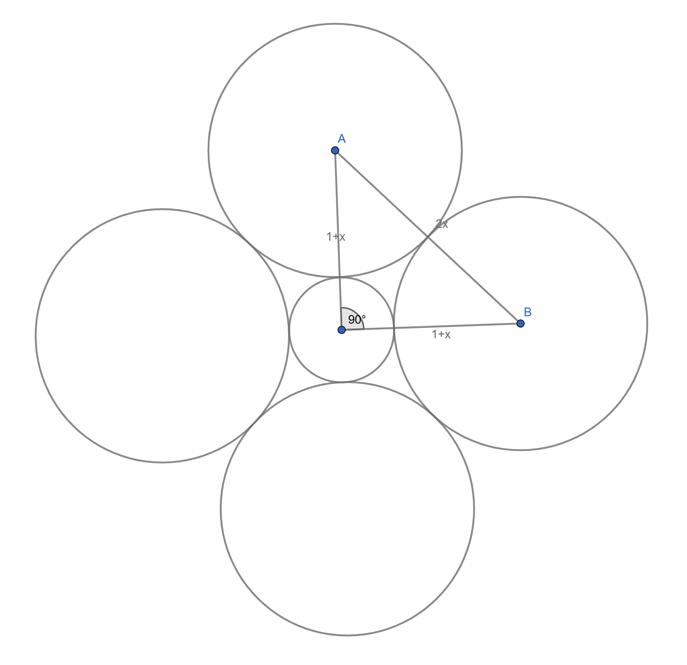
360^\circ / 4 = 90^\circ

Angle ACB is a right angle. Let the larger circles outside the centre circle have radius x.

Using the Pythagorean Theorem:

(1)   \begin{align*}(1+x)^2 + (1+x)^2 &= (2x)^2 \\2(x^2+2x+1) &= 4x^2 \\2x^2+4x+2 &= 4x^2 \\0 &= 2x^2-4x-2 \\0 &= x^2-2x-1\end{align*}

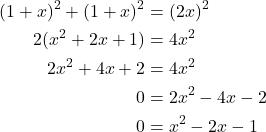
Using the Quadratic Formula:

(2)   \begin{align*}x &= \frac{2 \pm \sqrt{(-2)^2 - 4(1)(-1)}}{2} \\x &= \frac{2 \pm \sqrt{8}}{2} \\x &= \frac{2 \pm 2\sqrt{2}}{2} \\x &= 1 \pm \sqrt{2}\end{align*}

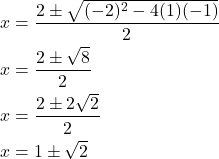
Since a length must be positive, x cannot be 1-\sqrt{2}.

Therefore x = 1+\sqrt{2}, and the radius is 1+\sqrt{2}.

c) Each circle around the centre circle must be tangent to the centre circle and 2 adjacent circles. Therefore, at least 3 circles around the centre circle must be required.

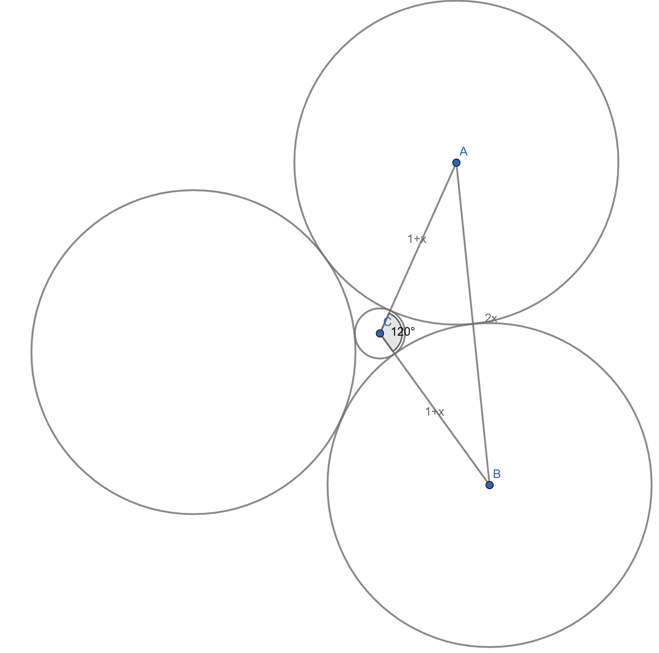
360^\circ / 3 = 120^\circ

Let the larger circles outside the centre circle have radius x.

Using the Law of Cosines:

(3)   \begin{align*}AB^2 &= AC^2 + BC^2 - 2(AC)(BC)(cos C) \\(2x)^2 &= (1+x)^2 + (1+x)^2 - 2(1+x)(1+x)(\cos120) \\4x^2 &= (1+x)^2 + (1+x)^2 - 2(1+x)^2(-\frac{1}{2}) \\4x^2 &= (1+x)^2 + (1+x)^2 + (1+x)^2 \\4x^2 &= 3(1+x)^2 \\4x^2 &= 3x^2 + 6x + 3 \\x^2 - 6x - 3 &= 0\end{align*}

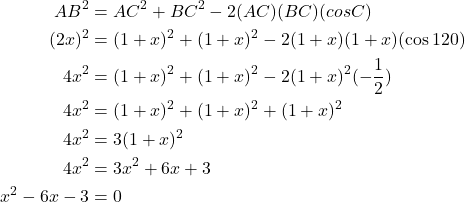
Using the Quadratic Formula:

(4)   \begin{align*}x &= \frac{6 \pm \sqrt{(-6)^2 - 4(1)(-3)}}{2} \\x &= \frac{6 \pm \sqrt{48}}{2} \\x &= \frac{6 \pm 4\sqrt{3}}{2} \\x &= 3 \pm 2\sqrt{3}\end{align*}

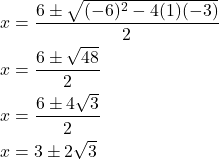
Since a length must be positive, x cannot be 3-2\sqrt{3}.

Therefore x = 3+2\sqrt{3}, and the radius is 3+2\sqrt{3}.

Site Search