Congratulations to Keo Osman from Simon Balle School in Hertford, Bruno Cerda-Mendoza from Sawston Village College, Rian Sarkar from Highgate School for successfully solving this problem!
(i)
Consider the triangle ![]() , where
, where ![]() and
and ![]() are the centres of two adjacent smaller circles.
are the centres of two adjacent smaller circles.
Let angle ![]() . Since similar triangles to
. Since similar triangles to ![]() can be made for each pair of adjacent circles, there are
can be made for each pair of adjacent circles, there are ![]() of these triangles, all with an angle
of these triangles, all with an angle ![]() .
.
Thus, ![]() . Taking one of these triangles we can split it into two right-angled triangles (as shown below).
. Taking one of these triangles we can split it into two right-angled triangles (as shown below).

Now considering triangle ![]() (where
(where ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() ), we see that
), we see that ![]() , as the radius of
, as the radius of ![]() plus the radius of one of the smaller circles.
plus the radius of one of the smaller circles.![]() , as the radius of one of the smaller circles. Let angle
, as the radius of one of the smaller circles. Let angle ![]() (and by symmetry
(and by symmetry ![]() ) =
) = ![]() .
.
From the previous conditions, we get that ![]() . From our previous condition of
. From our previous condition of ![]() , we also get
, we also get ![]() .
.![]() .
.![]()
![]() .
.
Note that, there were other valid formulas that we accepted, but this is the official solution.
(ii)
Circle B has radius ![]() , and thus area
, and thus area ![]() .
.
The area of each individual smaller circle is ![]() , thus their combined area is
, thus their combined area is ![]() .
.
It follows that ![]()
Plugging in our equation for ![]() found in part (i)
found in part (i) ![]()
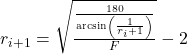
Starting with ![]() (the value of r is irrelevant here), after iterating many times you get
(the value of r is irrelevant here), after iterating many times you get ![]()
Plugging this back into our previous equation of ![]() yields
yields ![]() (if you iterate enough to find a good approximation of r).
(if you iterate enough to find a good approximation of r).