Problem of the Week

Problem 18 solution

Congratulations to William Chandler from Birchwood High School, Charlie Watkins, Felix Reiter from Bottisham Village College, Benjamin Heasley from Cambourne Village College and Prejeev Suhitharan from Harrow School for successfully solving this problem!

To solve this problem we break down the question into finding the surface area of the octahedron and the volume of cube.

To find the surface area of the octahedron we firstly find the side length of the octahedron. When we look at the middle cross section of the cube.

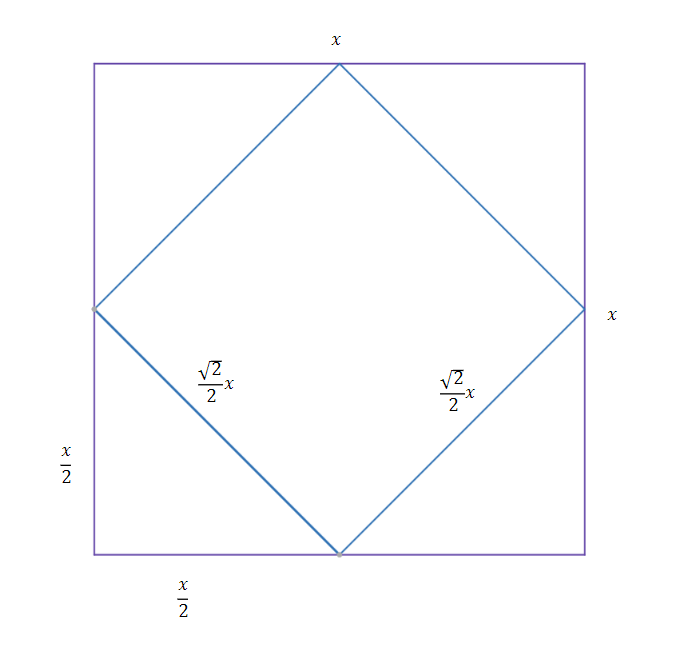
By using Pythagoras’ theorem

$\sqrt{\left(\frac{x}{2}\right)^2 + \left(\frac{x}{2}\right)^2} = \frac{\sqrt{2}}{2}x$

We find that the side length of the octahedron is

$\frac{\sqrt{2}}{2}x$

Now we look at one of the faces of the octahedron.

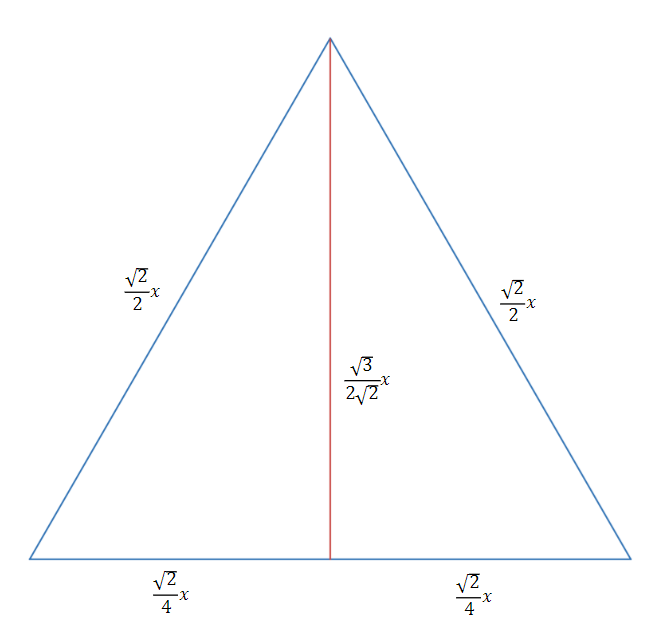
By using another Pythagoras’ theorem,

$\sqrt{\left(\frac{\sqrt{2}}{2}x\right)^{2}-\left(\frac{\sqrt{2}}{4}x\right)^{2}}=\frac{\sqrt{3}}{2\sqrt{2}}x$

We found that the height of the triangle is

$\frac{\sqrt{3}}{2\sqrt{2}}x$

Hence the area of the triangle is

$\frac{1}{2}bh$

$\frac{1}{2}\cdot\frac{\sqrt{3}}{2\sqrt{2}}x\cdot\frac{\sqrt{2}}{2}x=\frac{\sqrt{3}}{8}x^{2}$

An octahedron has 8 faces therefore the surface area will be

$8\cdot\frac{\sqrt{3}}{8}x^{2}=\sqrt{3}x^{2}$

Now we calculate the volume of a cube given side length $x$ . The volume would simply be

$x\cdot x\cdot x=x^{3}$

Therefore the ratio of the surface area of the octahedron: volume of cube is

$\sqrt{3}x^{2}\ :\ x^{3}$

which can be simplified into

$\sqrt{3}\ :\ x$

Submit a solution!

Name

Email

School / Institution

Details

Upload solution (*.jpg, *.pdf, *.docx, *.png accepted, max 2mb)

Publish consent

You can display my name on the CMS website if I successfully solve the problem.

Data Protection

I consent to providing this information to Cambridge Maths School. It will be processed in accordance with the Trust Privacy Policy.