i)
By drawing lines CE and BD you can create two triangles ECF and BFD. By the same segment theorem, angles FCE and FDB are equal. Similarly, angles FEC and FBD are equal. By the angle-angle similarity. These two triangles must be equal.
Therefore by considering the ratios of the sides we can deduce that 
.
Cross multiplying yields BF 
FC = EF FD.
ii)
The easiest way to solve this is to make a new construction where ED crosses the circle twice.
In this construction (diagram below) we can first create a cycling quadrilateral (as constructed by the green line segments FC and DB.
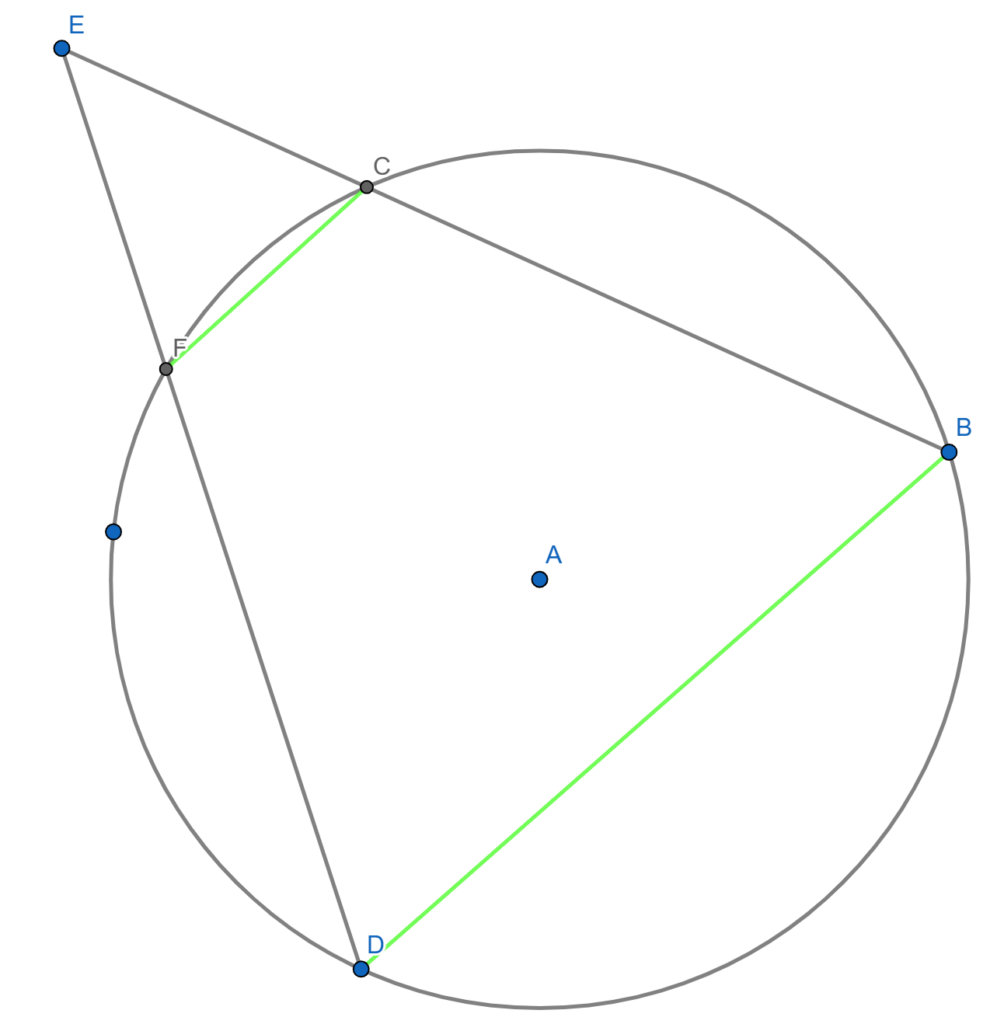
= 180 
(By opposite angles in a cyclic quadrilateral)
= 180 – 
= 
Similarly, 
EFC = DBC.
Thus, triangles EFC and EDB are similar.
Consequently, 
which implies EF FD = CB EC
When line ED is a tangent to the circle, EF = FD = ED
Thus, 
= CB EC
