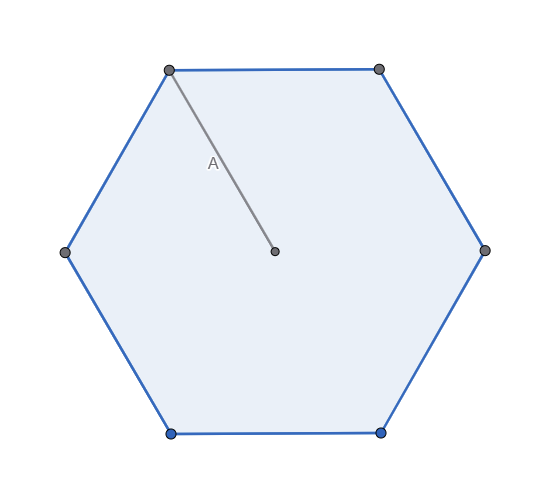
Let A be the length between a regular polygon’s centre to one of it’s vertices. An example of A is shown above for a regular hexagon.
a) Show that the area of a regular hexagon can be represented by ![]() .
.
b) Similarly, show that the area of a regular dodecagon (12-sided polygon) can be represented by ![]() .
.
c) Can an expression of the area be derived for a regular n-sided polygon, in terms of ![]() and
and ![]() ?
?
d) ![]()
![]() 2.598. As the number of sides in a regular polygon increases, the coefficient of
2.598. As the number of sides in a regular polygon increases, the coefficient of ![]() increases. State what the coefficient of
increases. State what the coefficient of ![]() approaches as the number of sides in a regular polygon increases more and more.
approaches as the number of sides in a regular polygon increases more and more.