Circle A is a circle of radius 
, centre C.
There exists n more circles, each of radius 1 arranged on the outside of Circle A such that each circle of radius 1 touches each of its neighbours and Circle A just once.
Circle B is a circle of centre C, with radius such that it touches each of the circles with radius one exactly once.
i) Find an equation linking the radius of Circle A, , and the number of circle radius 1. With as the subject.
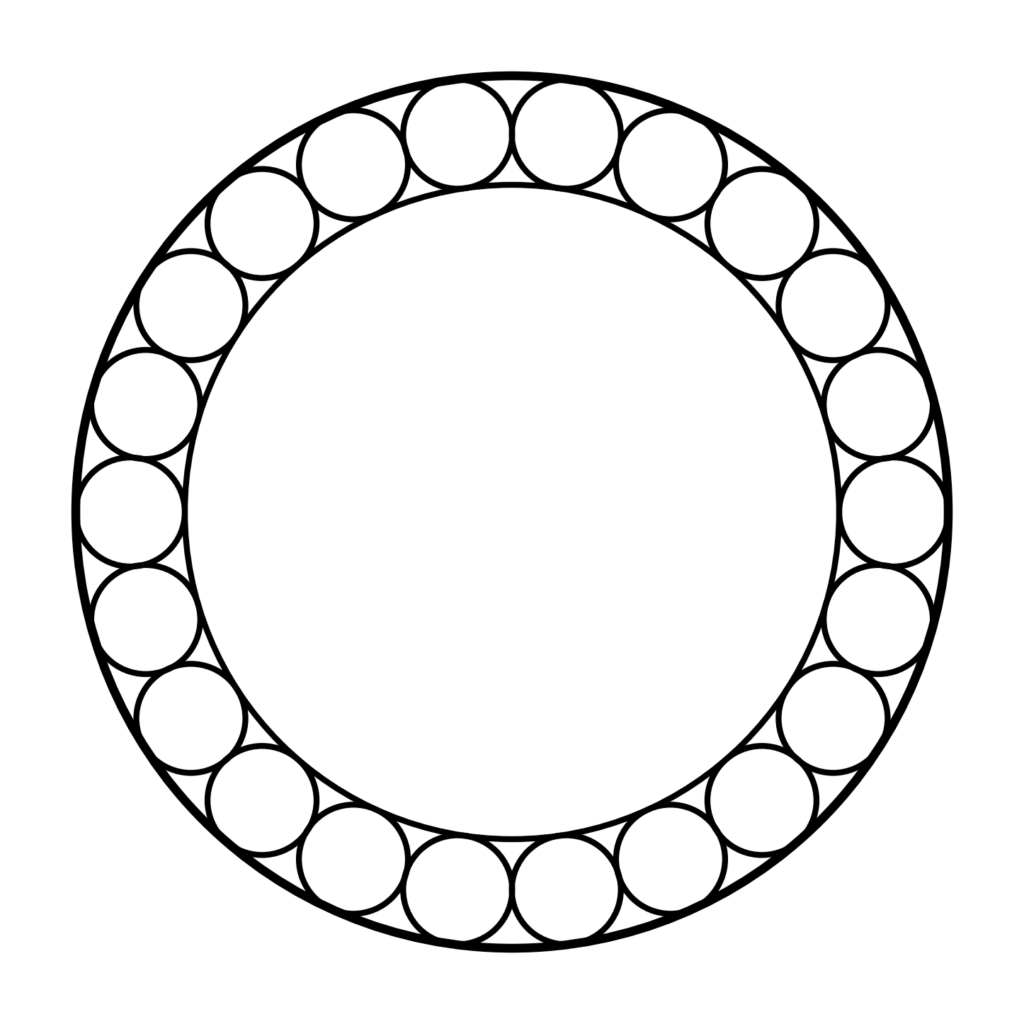
Note that the diagram above is just one example, the number of circles can increase.
ii) Circle B is centered at 
with radius 
. It touches each of the 
surrounding circles (radius 1) exactly once. All smaller circles are shaded, while circles A (radius ) and B remain unshaded.
Given that the fraction 
of the area of Circle B covered by the shaded circles is:
,
use an iterative method to estimate the radius of Circle A.
